Normal subgroup

In general, left and right cosets do not coincide for an arbitrary subgroup $H$. When they do, we say it is a normal subgroup:

Un subgrupo $H$ de un grupo $G$ se dice normal if $ghg^{-1} \in H$ para todo $g \in G$ and $h \in H$. Dicho de otra forma, $gHg^{-1}=H$.

Son aquellos que permiten hacer cociente y seguir obteniendo una estructura de grupo (this new group would act on the orbit space, not in the same space of course). **That is to say, they are made of transformations whose orbits get transformed to orbits of itself when any $g \in G$ is applied.

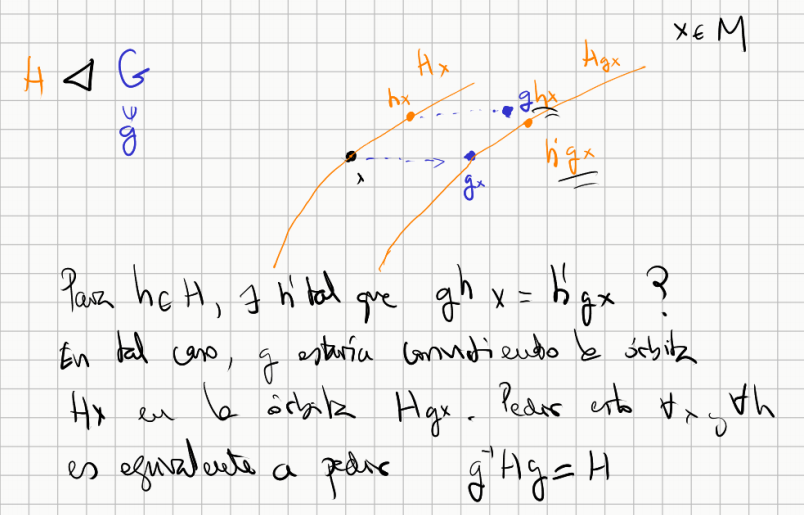
Suppose that $G$ acts on a manifold $M$. We can think of the space of orbits of $H$ acting on $M$. Being $H$ normal, an element $g\in G$ transforms complete orbits of $H$ into complete orbits of $H$.

I.E., WE CAN DEFINE AN ACTION OF THE QUOTIENT GROUP ON THE ORBITS SPACE!!! (I think it could be called quotient action)

At an infinitesimal level, the Lie algebra $\mathfrak{h}$ is an ideal of $\mathfrak{g}$. See the proof here

Por otro lado, su sentido visual es el siguiente.

Consideremos el grupo de simetrías de un cuadrado. Tiene ocho elementos:

donde se tienen las relaciones $s^2=1$, $rs=sr^3$, $r^2 s=s r^2$ (se visualiza mejor pensando que el cuadrado está en los números complejos con vértices: $-1, 1, i, -i$, y que $r$ es multiplicar por $i$ y $s$ es la conjugación).

Es sencillo comprobar que el sugbrupo $H=\{1,s\}$ no es normal, puesto que el grupo $rHr^{-1}=\{1,rsr^{-1}\}=\{1,r^2 s\}$ no coincide con $H$. Ambos grupos, aún no siendo iguales, tienen el mismo aspecto, en el sentido de que son el mismo pero trasladados.

Pues bien, un subgrupo normal es más "simétrico", en el sentido de que cualquier traslación de ida y vuelta lo deja como estaba. The subgroup $\{1, r, r^2, r^3\}$ is normal.

We can say that \textbf{a normal subgroup is an invariant set under the adjoint action of the group on itself}.

Normal subgroup as a kernel

If we have a group homomorphism $\phi: G\rightarrow G'$ the kernel $Ker(\phi)$ is a normal subgroup (easy to proof). But conversely, if $H \triangleleft G$ we can see $H$ as the kernel of the map

This can be visualized in terms of the action of $G$ over a set $M$. If $G$ has a normal subgroup $H$, then we can define a group $G^{orb}$ acting on the space $M^{orb}$ of orbits of $H$ (see above). Every $g\in G$ can be seen as an element of $G^{orb}$ and the kernel of this association is, obviously $H$. So, for me, the essence of normal subgroups is that they let us to comprise the space $M$ to an orbit space and an the group $G$ to an orbit group acting on the orbit space.

________________________________________

________________________________________

________________________________________

Author of the notes: Antonio J. Pan-Collantes

antonio.pan@uca.es